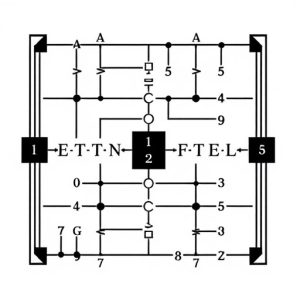
In the digital world, the full adder circuit, built with logic gates (AND, OR, NOT), is a fundamental building block for binary addition. It combines inputs (binary numbers A & B, carry-in Cin) to produce Sum and carry-out Cout, essential for complex computational tasks. Logic gates themselves are vital, each having a unique function: AND requires both inputs, OR activates on at least one input, and NOT inverts the signal. Understanding these gates is key to designing advanced digital systems. Designing a full adder involves strategically combining these logic gates. Efficiency optimization techniques enhance performance, ensuring robust operation. Full adder circuits power complex arithmetic operations across diverse tech fields, from processors to AI, making them indispensable for modern computing.
Discover the fundamental building block of digital arithmetic—the full adder circuit, crafted meticulously from logic gates. This article explores the intricate world of logic gates—AND, OR, and NOT—unveiling their pivotal role in designing efficient full adders. We’ll guide you through a step-by-step process of creating this essential circuit, followed by optimization techniques for enhanced performance. Beyond theory, we delve into real-world applications, showcasing the versatility of full adders in modern digital systems.
- Understanding Full Adder: The Building Block of Digital Arithmetic
- Logic Gates: AND, OR, and NOT – The Fundamentals
- Designing a Full Adder Using Logic Gates: Step-by-Step
- Optimizing the Circuit: Techniques for Efficient Implementation
- Applications and Beyond: Exploring Full Adders in Digital Systems
Understanding Full Adder: The Building Block of Digital Arithmetic
In the realm of digital arithmetic, the full adder circuit stands as a fundamental building block, meticulously constructed using logic gates to perform addition. This intricate circuit is responsible for accurately summing two binary numbers and generating a carry signal, making it an indispensable component in various computational processes. By combining and manipulating different logic gates, such as AND, OR, and NOT, designers create full adder circuits capable of handling binary arithmetic operations with precision and efficiency.
Each full adder circuit comprises three inputs: two for the binary numbers being added (A and B) and one for the carry-in signal (Cin). The circuit’s output includes a sum (Sum) and a carry-out signal (Cout), which are crucial for subsequent computational steps. Understanding how logic gates interact within this circuit is essential to grasp the broader concepts of digital design, as it forms the basis for more complex arithmetic operations and overall system functionality.
Logic Gates: AND, OR, and NOT – The Fundamentals
Logic gates are fundamental building blocks in digital electronics, forming the basis for complex circuits and systems. These elementary components perform specific logical operations on binary inputs, producing outputs based on defined rules. The three primary logic gates are AND, OR, and NOT, each with its distinct functionality.
The AND gate is a basic building block that requires both input signals to be active (typically represented as 1) for an output of 1. It represents conjunction or the need for multiple conditions to be met simultaneously. In contrast, the OR gate activates its output when at least one input is active, symbolizing alternative or the option for any condition to trigger a result. Conversely, the NOT gate inverts the input signal; a 1 becomes a 0, and vice versa, indicating negation or complementation. Understanding these fundamental logic gates is crucial when designing more complex circuits, as they can be combined to create full adders and other advanced digital systems.
Designing a Full Adder Using Logic Gates: Step-by-Step
Designing a Full Adder Using Logic Gates involves a systematic process, allowing engineers and enthusiasts alike to create this essential digital building block. The first step is to identify the required logic gates for each component of the adder—the sum and carry outputs. Typically, this includes AND, OR, and NOT gates, which are the fundamental units in constructing more complex circuits.
The adder’s design then proceeds with a logical flow. You’ll need to consider how these gates interact and connect to achieve the desired addition. For instance, a full adder requires three inputs: two bits for addition (A and B) and one carry-in bit. By combining AND and OR gates, you can create summing circuits that compute A+B, while NOT gates are employed to handle the carry propagation from bit to bit. This step-by-step approach ensures a structured design, enabling precise control over the circuit’s functionality and behavior.
Optimizing the Circuit: Techniques for Efficient Implementation
In designing a full adder circuit using logic gates, optimizing efficiency is paramount. Techniques such as gate sizing and placement play a significant role in minimizing power consumption and maximizing speed. By carefully selecting the types and sizes of logic gates, engineers can tailor the circuit to specific performance requirements. For instance, utilizing larger transistors for critical paths can reduce propagation delays, ensuring faster sum and carry signals.
Additionally, logical optimization methods like Boolean algebra and Karnaugh maps aid in simplifying complex circuits. These tools help identify redundant operations and spare logic gates, streamlining the design process. Efficient implementation also involves minimizing wire lengths to reduce signal degradation and crosstalk, which is a major concern in high-density integrated circuits. This ensures robust performance across various operating conditions, making the full adder circuit more reliable and versatile.
Applications and Beyond: Exploring Full Adders in Digital Systems
In the realm of digital systems, full adder circuits powered by logic gates are indispensable components that facilitate complex arithmetic operations. Their versatility extends beyond simple addition; they form the backbone for implementing more intricate mathematical functions like multiplication and division in digital signal processors, microprocessors, and other embedded systems. By combining various logic gates such as AND, OR, NOT, and XOR, engineers can design full adder circuits tailored to specific computational requirements.
Beyond their fundamental role in arithmetic operations, full adder circuits with logic gate integrations play a pivotal role in modern technology. They are integral to the functioning of high-performance computers, contributing to faster processing speeds and enhanced computational capabilities. Furthermore, these circuits find applications in areas like telecommunications, cryptography, and artificial intelligence, where accurate and efficient number-crunching is paramount. Their ability to process binary digits with precision makes them invaluable assets in today’s digital landscape.
