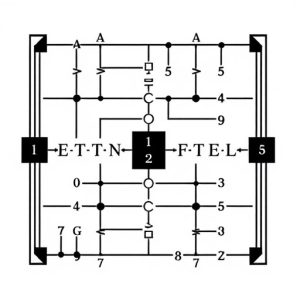
Full adder circuits, core components in digital electronics for binary addition, utilize logic gates (AND, OR, NOT) to efficiently perform arithmetic operations. These gates enable sum calculation and carry propagation, accurately handling diverse binary inputs. Carrying and overflow mechanisms, implemented using specialized gates, ensure robust circuit performance even with sums exceeding representable values. Designing full adders involves strategic gate selection, signal integrity management, load balancing, and power optimization for efficient, reliable digital system operations.
Explore the fundamental building blocks of digital systems with this in-depth guide to full adder circuits using logic gates. We’ll unravel the intricacies of binary addition, demystify the role of AND, OR, and NOT gates, and design efficient sum and carry logic. Learn how to implement carrying and overflow mechanisms for robust circuit design. Discover practical considerations that make full adder implementation accessible, enhancing your understanding of digital logic gates and their applications.
- Understanding Binary Addition and Full Adders
- Building Blocks of a Full Adder: AND, OR, and NOT Gates
- Designing the Sum and Carry Logic
- Implementing Carrying and Overflow Mechanisms
- Practical Considerations for Full Adder Circuit Design using Logic Gates
Understanding Binary Addition and Full Adders
Binary addition forms the fundamental basis for understanding full adder circuits, which are crucial components in digital electronics relying on logic gates. In binary, numbers are represented using only two digits, 0 and 1, making it a base-2 number system. When adding two binary numbers, each digit is aligned, and the sum is determined based on the traditional addition rules but limited to these two values.
Full adders are specifically designed logic circuits that perform this binary addition. They take in two binary inputs and a carry bit from the previous stage and produce the sum and a new carry bit as outputs. By using various logic gates, such as AND, OR, and NOT, full adder circuits efficiently execute these additions, ensuring accurate calculations in digital systems.
Building Blocks of a Full Adder: AND, OR, and NOT Gates
The full adder circuit is a fundamental building block in digital electronics, responsible for performing arithmetic operations, particularly addition. At its core, this complexity is achieved through the strategic combination of simpler logic gates. The primary logic gates employed in a full adder are AND, OR, and NOT, each playing a crucial role in the addition process.
The AND gate, as the name suggests, performs the logical conjunction operation, outputting 1 only when both inputs are 1. This is essential for controlling the carry signal in binary addition. The OR gate, on the other hand, executes the logical disjunction, returning 1 if at least one of its inputs is 1, which is vital for summing the bits. NOT gates reverse the state of their input, making them indispensable for adjusting the bit values during the addition process. Together, these logic gates orchestrate the intricate dance of binary addition within the full adder circuit.
Designing the Sum and Carry Logic
When designing the Sum and Carry Logic for a full adder circuit, the primary goal is to leverage various logic gates to achieve both functions simultaneously. The sum part involves adding two binary digits, while the carry part determines if there’s a transfer of excess ones from one bit position to the next. AND gates are commonly used to determine if each digit contributes to the sum, while OR gates facilitate the carry signal based on the output of the AND operations and the previous carry bit.
By combining these logic gates strategically, the circuit ensures accurate sum calculation and proper carry propagation. This design must account for all possible binary inputs (00, 01, 10, 11) to produce the correct sum and carry outputs. Each gate’s logical behavior is meticulously arranged to mirror the arithmetic addition process, resulting in a robust full adder circuit capable of handling diverse input scenarios effectively.
Implementing Carrying and Overflow Mechanisms
Implementing carrying and overflow mechanisms is a crucial aspect of designing a full adder circuit using logic gates. Logic gates, such as AND, OR, and NOT, play a pivotal role in these mechanisms by enabling the proper propagation and accumulation of binary values. For instance, when adding two binary numbers, a carry bit is generated for each column position, indicating the sum’s excess over 1. This carry signal is fed into the next higher-order bit position, ensuring accurate representation of the final result.
To handle overflow, which occurs when the sum exceeds the maximum value representable by the adder circuit, specialized logic gates are employed. These gates detect conditions where the output of the addition surpasses the expected range and trigger appropriate responses. By combining various logic gate configurations, such as XOR and AND, with careful signal routing, engineers can design circuits that not only perform accurate additions but also intelligently manage carry and overflow conditions, enhancing the overall robustness and reliability of digital systems.
Practical Considerations for Full Adder Circuit Design using Logic Gates
When designing a full adder circuit using logic gates, it’s crucial to consider the practical implications that will affect performance and efficiency. The choice of logic gates plays a significant role; different types like AND, OR, NOT, and XOR gates have unique characteristics that influence the speed and power consumption of the circuit. For instance, modern technologies often prefer lower-power logic gates for energy-efficient designs, especially in integrated circuits where space is limited.
Additionally, signal integrity must be addressed to ensure accurate calculations. As signals pass through multiple gates, noise and interference can accumulate, leading to faulty results. Proper routing techniques, including proper ground planes and power distribution, help mitigate these issues. Balancing the load of each gate is also essential; unequal signal strengths across gates can cause timing discrepancies, affecting the overall speed and stability of the full adder circuit.
