Exploring Reversible Logic Gates: Functions, Designs, and Quantum Applications
Reversible logic gates are fundamental components that enhance modern digital systems by allowing c…….

Reversible logic gates are fundamental components that enhance modern digital systems by allowing computations to be reversed, thereby preserving input values and state information. These gates play a crucial role in quantum computing by maintaining quantum coherence, improving error correction, and fault tolerance. Unlike traditional logic gates, which irrevocably change inputs, reversible gates offer energy efficiency, reduced heat production, and data integrity benefits across classical and quantum domains. They are essential for complex permutations in cryptography, contribute to high-density storage with non-volatile memory, and align with sustainability goals by being less resource-intensive. Reversible logic gates also facilitate more secure and efficient computational processes by eliminating data loss and vulnerabilities associated with traditional operations, making them a cornerstone for future advancements in computing technology, including quantum algorithms like Grover's and Shor's, which they help to execute more efficiently. Their reversibility leads to less complex circuit designs and contributes to the overall development of secure, energy-efficient, and robust computational systems.
Explore the intricate realm of reversible logic gates, a pivotal component in advanced computational systems. This article delves into their functions and diverse applications, unraveling their significance in modern technology. We’ll navigate the mathematical underpinnings that govern these devices, elucidating the principles of Boolean logic and permutation patterns they adhere to. Further, we’ll examine the design and implementation strategies that make reversible logic gates a cornerstone for efficient circuitry. Their advantages, particularly in bolstering security and optimizing resources within computational systems, are also highlighted. Finally, a comparative analysis sets reversible against irreversible logic gates, casting light on their integral role in the burgeoning field of quantum computing. Join us as we dissect the science behind these transformative elements of digital logic.
- Understanding Reversible Logic Gates: A Primer on Their Functions and Applications
- The Mathematical Foundations of Reversible Logic Gates: Exploring Boolen Logic and Permutation Paradigms
- Design and Implementation of Reversible Logic Gates: Strategies for Efficient Circuitry
- Advantages of Reversible Logic Gates in Computational Systems: Enhancing Security and Resource Optimization
- Comparative Analysis: Reversible vs. Irreversible Logic Gates and the Role in Quantum Computing
Understanding Reversible Logic Gates: A Primer on Their Functions and Applications

Logic gates are fundamental components in digital circuits, enabling binary operations that form the backbone of computing devices. Unlike their irreversible counterparts, reversible logic gates have a unique property: they can recover the inputs from their outputs. This characteristic is particularly beneficial in error correction and fault-tolerant systems within quantum computing, where maintaining quantum coherence is paramount. In classical digital systems, traditional logic gates irrevocably alter the state of the input signals to produce an output, making reversible gates less intuitive but more essential in specific contexts where partial information about past states can be exploited for system resilience and data integrity.
The functions of reversible logic gates are diverse and extend beyond quantum computing applications. They play a critical role in coding theory, cryptography, and certain secure data transmission protocols. In these fields, the ability to implement reversible operations allows for more robust and secure systems. For instance, in cryptographic algorithms, reversible gates can help in creating complex permutations that are difficult to reverse without the correct key, thus enhancing encryption methods. Additionally, in the realm of computer architecture, reversible logic gates can contribute to designing more efficient processors that consume less energy and produce less heat compared to their irreversible counterparts. This not only aids in environmental sustainability but also opens avenues for performance improvements in high-density computing environments.
The Mathematical Foundations of Reversible Logic Gates: Exploring Boolen Logic and Permutation Paradigms

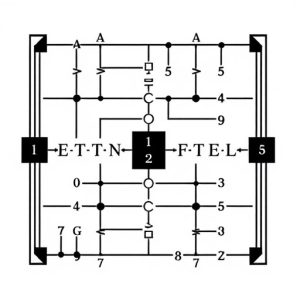
In the realm of digital circuitry, reversible logic gates play a pivotal role in computing architectures, particularly where data non-volatility and storage density are paramount. The mathematical underpinnings of these gates are deeply rooted in Boolean logic, a binary system of thought that represents variables as either true or false, 1 or 0. This binary representation simplifies complex logical problems into a set of algebraic equations known as Boolean expressions. These expressions form the basis for constructing digital circuits, including reversible logic gates, which unlike their irreversible counterparts, preserve the input data upon computation.
The concept of reversibility in logic gates is closely tied to the notion of permutation paradigms. In essence, a permutation paradigm involves a transformation where each input value maps to a unique output value, and every output value corresponds to a single input value. This bijective nature ensures that no information is lost, making it an ideal framework for reversible logic gate design. The mathematical elegance of permutation logic extends beyond individual gates to entire circuits, enabling the creation of systems capable of universal computation without the need for flip-flops or feedback loops typically required in irreversible designs. This not only conserves energy but also reduces the complexity and potential for errors within high-density storage applications. The exploration of reversible logic gates is a testament to the ingenuity of digital design, where mathematical principles intersect with technological innovation to push the boundaries of computing capabilities.
Design and Implementation of Reversible Logic Gates: Strategies for Efficient Circuitry

In the realm of computer science and digital circuits, the concept of reversible logic gates has garnered significant attention due to their unique advantages over traditional irreversible logic gates. The design and implementation of these gates are centered around the principle that each operation can be both executed and reversed, allowing for a new dimension of computational potential. Reversible logic gates operate on the principle that every logical input has a corresponding inverse operation that can recover the original state. This characteristic is particularly advantageous in quantum computing, where information cannot be destroyed but must be transformed without loss during computation. The implementation of these gates involves careful consideration of their ability to perform such inverse operations while maintaining the integrity and flow of data through the circuit.
The strategies for efficient circuitry with reversible logic gates focus on minimizing the complexity and resource overhead often associated with quantum algorithms. By leveraging the concept of reversibility, designers can create circuits that are both smaller and faster compared to their irreversible counterparts when performing certain types of computations. One key strategy is the use of fewer bits for inputs and outputs, as each bit in an irreversible gate requires a complementary bit to maintain state, which doubles the resource requirement. In contrast, reversible gates can maintain all information with fewer bits due to their one-to-one mapping of input to output. Additionally, the design must account for the logical reversibility operations, such as the Fredkin gate and the Toffoli gate, which are fundamental components in constructing more complex reversible logic circuits. These gates enable the selective swapping or copying of bits without losing any information, thus ensuring the reversibility of the circuit. As a result, the design and implementation of reversible logic gates represent a significant step forward in creating more efficient and resource-optimized computational devices.
Advantages of Reversible Logic Gates in Computational Systems: Enhancing Security and Resource Optimization

Reversible logic gates represent a significant advancement in computational systems, offering distinct advantages over their irreversible counterparts. One of the primary benefits is their role in enhancing security within digital architectures. Traditional logic gates, such as AND, OR, and NOT, irrevocably alter the state of information they process. This one-way operation can leave traces that may be exploited by attackers to reconstruct sensitive data through side-channel attacks or similar methods. In contrast, reversible logic gates allow for the exact recovery of input states, thereby enabling a higher level of security as any manipulation of data can be fully undone, leaving no permanent record of the information processed. This characteristic is particularly valuable in cryptographic applications where maintaining the confidentiality and integrity of data is paramount.
Furthermore, reversible logic gates contribute to resource optimization within computational systems. By virtue of being non-destructive, they can minimize energy consumption and reduce the complexity of error correction mechanisms required in quantum computing. The ability to reuse information without degradation means that less information needs to be stored redundantly to compensate for losses, leading to more efficient use of memory resources. This optimization extends beyond energy and storage; it also impacts the computational speed and the design complexity of circuits. As the field of computing continues to evolve towards more sophisticated and integrated systems, the principles of reversible logic gates will play a crucial role in achieving greater efficiency and performance while maintaining stringent security standards. Logic gates that embody these principles are not just a response to current computational challenges but a foundational element for the future of secure and efficient computing.
Comparative Analysis: Reversible vs. Irreversible Logic Gates and the Role in Quantum Computing

Reversible logic gates occupy a pivotal role in quantum computing, distinguishing themselves from their classical counterparts through an intrinsic ability to undo computations. This feature is not just a theoretical curiosity but a practical necessity for quantum systems, which must maintain the integrity of quantum information throughout a computation. In stark contrast, irreversible logic gates, as used in traditional digital circuits, irrevocably alter the state they process. While these gates are efficient for classical binary computations, their one-way nature can lead to issues with error accumulation in quantum systems. Reversible logic gates, on the other hand, utilize fewer gates to perform operations compared to their irreversible counterparts when implemented in certain contexts. This efficiency is compounded by their ability to act as both an operation and its inverse, allowing for the reversal of computational steps, which is crucial for quantum error correction and the implementation of quantum algorithms like Grover’s or Shor’s algorithms. The concept of reversibility extends beyond just the gates themselves; it permeates the entire architecture of quantum computing, from fundamental principles to the intricate designs of quantum circuits. As such, understanding and harnessing the properties of reversible logic gates is essential for advancing the field of quantum computing.