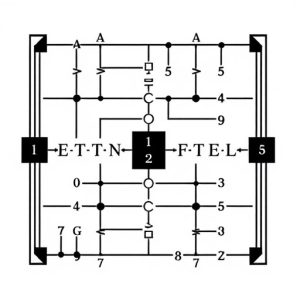
Crafting Full Adders: A Step-by-Step Guide Using Logic Gates
Binary addition, a fundamental operation in digital electronics, relies on full adder circuits compo…….

Binary addition, a fundamental operation in digital electronics, relies on full adder circuits composed of AND, OR, and NOT logic gates to perform arithmetic tasks. These gates process input bits to generate sum and carry signals, with half adders serving as building blocks for the full adder structure. Designing a full adder involves meticulous integration of these gates, while verification and optimization processes ensure accurate circuit performance through logical design analysis, ultimately enhancing computational capabilities in modern digital systems by leveraging logic gates as foundational elements.
Discover the fundamentals of binary addition and explore the power of full adders in digital circuit design. This article delves into the intricate world of logic gates, showcasing their role as building blocks for complex circuits. We’ll guide you through the process of designing and implementing a full adder step-by-step, providing insights on optimizing its performance. By understanding the interplay of logic gates, readers will gain valuable knowledge to create efficient digital systems.
- Understanding Binary Addition and Full Adders
- Building Blocks of a Full Adder Circuit
- Designing the Logic Gates for a Full Adder
- Implementing the Circuit: Step-by-Step Guide
- Verifying and Optimizing the Full Adder Circuit using Logic Gates
Understanding Binary Addition and Full Adders

Binary addition is a fundamental concept in digital electronics, representing the process of combining two binary numbers to produce their sum. In the context of logic gates, understanding binary addition is crucial as it forms the basis for more complex arithmetic operations. A full adder circuit is an essential building block in this realm, designed to perform binary addition and provide a sum output along with a carry signal.
This circuit comprises multiple logic gates, each playing a specific role in the addition process. Logic gates, such as AND, OR, and NOT, are combined to create the full adder, enabling the manipulation of binary bits. The primary function is to add two binary digits (bits) and a carry from a previous stage, resulting in a sum bit and a new carry value. By employing these logic gates, digital systems can perform arithmetic operations, making them indispensable for various computational tasks within modern electronics.
Building Blocks of a Full Adder Circuit

The full adder circuit, a fundamental building block in digital electronics, is crafted from simple yet powerful components—logic gates. These gates, serving as the backbone of the circuit’s functionality, perform specific logical operations that collectively enable addition of binary numbers. Among the key logic gates employed are AND, OR, and NOT gates, each contributing unique functions. The AND gate, for instance, ensures both input bits must be 1 for a 1 output, while the OR gate produces a 1 output when either or both inputs are 1. The NOT gate, conversely, inverts the input signal, changing a 1 to 0 and vice versa.
Arranging these logic gates in strategic configurations allows for the realization of various operations within the full adder. For instance, half adders, composed of two AND gates, an OR gate, and a NOT gate, form the circuit’s fundamental units. These half adders then combine to create the final full adder, capable of summing two binary digits with carry signals. This hierarchical structure not only simplifies design but also enhances understandability, making it easier to debug and optimize circuit performance through meticulous logic gate arrangement.
Designing the Logic Gates for a Full Adder

Designing the logic gates for a full adder involves carefully crafting each gate to perform specific arithmetic operations. A full adder takes three binary inputs (a, b, and carry-in) and produces two outputs (sum and carry-out). It combines these inputs to achieve addition, making it a fundamental building block in digital electronics.
Each logic gate, such as AND, OR, and NOT, plays a crucial role in this process. The AND gate checks if both ‘a’ and ‘b’ are 1s, contributing to the sum output. The OR gate determines if either ‘a’ or ‘b’ (or both) is 1, influencing the carry-out. The NOT gate, or inverter, inverts the carry-in signal, ensuring proper signal flow. By combining these gates, engineers can create a robust full adder circuit capable of accurately performing binary addition.
Implementing the Circuit: Step-by-Step Guide

Implementing the full adder circuit involves a systematic approach using basic logic gates. Start by designing the carry lookup table (CLUT), which determines the carry-out signal based on the inputs. Utilize AND and OR gates to create this table, ensuring each possible combination of bit inputs has a corresponding output. Next, construct the sum-of-products sections, employing AND gates to multiply the input bits by 1 or 0 based on the CLUT outputs. These products are then summed using further OR gates to produce the final sum and carry signals.
Connect these components in a sequential manner, ensuring proper signal flow from one stage to the next. Test your circuit by inputting various binary numbers and verifying the correct output for both the sum and carry. This step-by-step process allows you to build a robust full adder capable of performing addition operations using only fundamental logic gates.
Verifying and Optimizing the Full Adder Circuit using Logic Gates

Verifying the functionality of a full adder circuit constructed with logic gates is a meticulous process. It involves employing techniques such as truth tables and simulation to ensure each gate operates as expected under various input conditions. By comparing the circuit’s output against predefined results, engineers can identify any discrepancies and pinpoint areas needing adjustment. This verification step is crucial for ensuring the reliability of the circuit in real-world applications.
Optimization comes next, focusing on enhancing the circuit’s performance and efficiency. Through logical design analysis, engineers can identify redundant gates or inefficient operations, replacing them with more streamlined alternatives. Additionally, power consumption and heat dissipation considerations come into play, driving the design towards a more energy-efficient and thermally manageable solution. Logic gates, being fundamental building blocks, play a pivotal role in both verification and optimization phases, ultimately shaping the full adder circuit’s overall performance and robustness.